| <-- Previous | Contents Page | Next --> |
The Earth is closer to an Ellipsoid than it is to a sphere. The density varies, causing the centre of gravity to be not quite at the geometric centre. However, for rough purposes we can ignore the complications and use a sphere of uniform density as a good approximation.
The Earth spins on an axis which runs through the centre and emerges at the Poles. Due to this spin, the Sun rises in the east, sets in the west and traverses the sky via the south and away from the north. That gives us the cardinal points of the compass.
Which way up we draw the Earth is entirely arbitrary. Before the magnetic compass was invented, European maps were drawn with east at the top and Jerusalem at the centre. Muslims centred their maps on the holy city of Mecca. Nowadays we follow a convention that the Earth is drawn with the North Pole at the top:
This convention is so embedded in our brains that during the Apollo Moonshot programme, when the astronauts looked back at the Earth, they couldn't understand what they were seeing at first, because the North Pole was not at the top of the Earth.
The Earth's magnetic field is aligned approximately with the axis of spin and so the needle of a magnetic compass also aligns itself with that axis. We tend to say that the needle of a compass points to the north but I have no idea why somebody decided that. Strictly one end points to the North Pole and the other end points to the South Pole.
The Equator is the line around the Earth on which every point is equidistant from the Poles. Imagine a plane perpendicular to the axis of spin which passes through the centre. Where that plane meets the Earth's surface is the Equator:

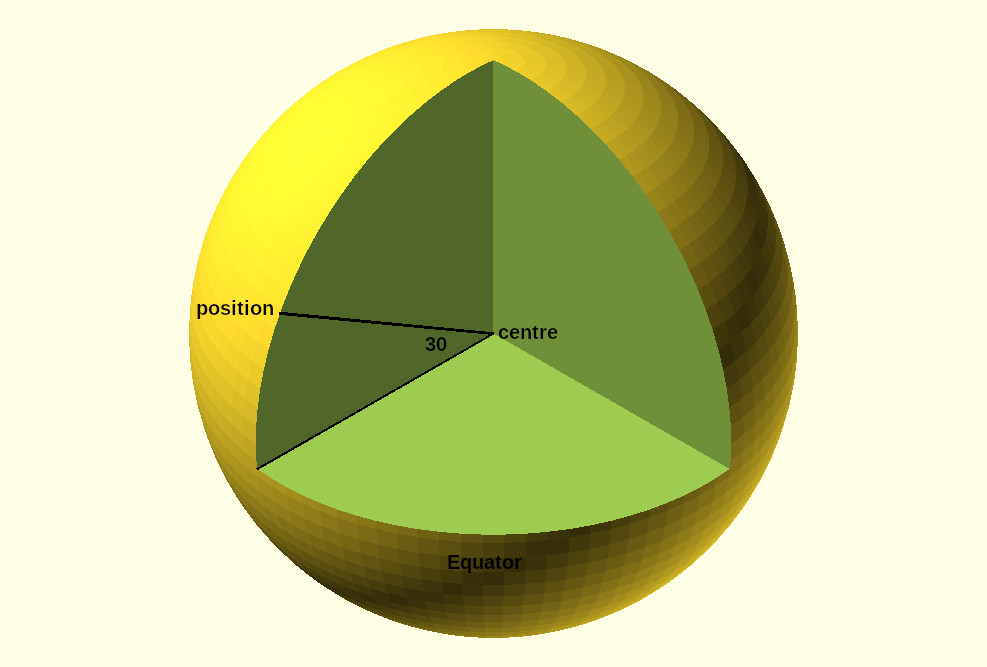
Once we've established those observations and conventions, we can start to define positions on the surface of the Earth using numbers. Given a position we draw a circle around the surface from Pole to Pole (a meridian) passing through our position. We draw a straight line from the centre of the Earth to our position and another straight line from the centre to the point where the meridian meets the Equator. The angle between the two straight lines is the Latitude of the two points. We could express the angle in radians but the convention is to use degrees.
For example this position is at latitude 30°:
GNSS devices often report their position in one or other of these formats. If you have two devices and they use different formats, that can be interesting. If you're lucky, they might give you a choice of format. If not you can use this web page to convert from one to the other.
Within this framework, any point on the Equator has latitude 0° and the latitude value increases as you approach the North Pole. If you move to the south of the Equator, your angle of latitude goes negative. The North Pole is at latitude 90°, the South Pole is at latitude -90°.
This gives us the familiar lines of latitude (or parallels) running around the Earth east to west. All points on one of those circles are at the same latitude:
The Earth has radius 6,371,000 metres. On a perfectly spherical planet, the meridians would all be circles of that radius.
The length taken up by one degree of latitude from north to south around the surface of a spherical version of the Earth is:
2 X pi X radius
A spreadsheet such as Microsoft Excel can do the necessary calculation. Excel has a handy gadget PI(), which is the value of pi to the best accuracy that your computer can manage. So you can calculate the length taken up by one degree of latitude from north to south around the surface of a spherical version of the Earth using this Excel formula:
=((2*PI()*6371000)/360)
which gives the result 111,194.9266 metres.
You can measure latitude in degrees, as is the convention, but you could just as easily measure it in terms of distance around the meridian from the Equator.
The circumference of a circle is
diameter X piso the circumference of a meridian is about 40,030,174 metres.
That's not really a surprise because the metre was originally defined as one ten millionth of the distance along a meridian passing through the Paris Observatory from the Equator to the North Pole - a trip one quarter the way around the Earth. If the Earth was a perfect sphere the circumference would be exactly 40,000,000 metres, but it isn't a perfect sphere.
Given all that, we can do some rough calculations:
If my GNSS receiver is accurate to two or three centimetres, I should round the value up to three decimal places and ignore the rest.
We can mark a position east to west in a similar way using meridians called lines of longitude:
Positions of the lines of latitude are fixed relative to the Equator, which is an artifact of the Earth's spin, so we have no choice where to put them. On the other hand, the positions of the lines of longitude are arbitrary. We draw one of them through a chosen position on land and call it the Prime Meridian. Positions on that meridian are at longitude 0°. The others are relative to that. Where we put the Prime Meridian is entirely down to convention.
We have to make another arbitrary decision, which is the direction of increase and decrease of longitude. By convention, positions to the east of the Prime Meridian have a positive longitude value and positions to the west of it have a negative longitude value. The meridian opposite to the Prime Meridian is at longitude 180° and runs close to New Zealand and through the eastern end of Siberia.
Longitude values can be marked E and W instead of positive and negative, for example the W90° or -90° meridian crosses Guatemala.
Why does the Prime Meridian run through Greenwich? It makes sense to define it using observations of the position of the stars, then you can find your own longitude by the same method. So your Prime Meridian runs north-south through an observatory, actually through its most accurate telescope.
In the Nineteenth Century, Britain had the most powerful navy in the world - Britannia ruled the waves. The British Admiralty put a lot of money into making navigation tables and so they got to decide the convention that we still use today. The Prime Meridian runs through the site of the telescope at the Royal Greenwich Observatory in London which was used to define it.
In fact, I'm told that the Observatory has moved the Prime Meridian a few metres at least once when they built a better telescope next to the old one and started to use that instead.
Eventually the Observatory put a line on the ground marking the path of the Prime Meridian but as explained here it was in the wrong position from the first and it's moved a bit more since due to continental drift.
If maps had been standardised in another era, the Prime Meridian might have run through the Paris Observatory or through the United States Naval Observatory in Washington DC, depending on which nation had the most clout at the time.
This page from the UK Open University explains how to use some very simple equipment to find your longitude and latitude relative to the Prime Meridian and the Equator. The more accurate your measuring equipment and clock, the more accurate will be your result.
If two positions have the same latitude and different longitudes, one is due east of the other and they lie on the same circle of latitude.
(A change in your longitude moves you along a circle of latitude and a change in your latitude moves you along a circle of longitude! This confused me at first.)
We can calculate the distance covered by a degree of longitude as we did earlier for a degree of latitude but because the circles of longitude are all of different sizes, the answer depends on your latitude.
I live in the UK, which lies between the 50 degree parallel and the 60 degree parallel. For a rough estimate we can work out the length of one parallel and use that result everywhere in the UK. 55 degrees latitude is in the middle, so I will use that. The fair cities of Newcastle-upon-Tyne and Belfast are both close to this parallel. According to Wikipedia, the centre of Newcastle is at latitude 54° 58' 42' and the centre of Belfast is at 54° 35′ 49″.
To work out the length of the 55 degree parallel, use this picture:
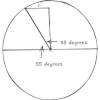
We know the length of the hypotenuse of the right-angled triangle in the picture. It's the radius of the Earth, 6,371,000 metres. We're interested in the length r, the radius of the 55 degree parallel.
The sine of an angle is:
(length of opposite side) divided by (length of hypotenuse),
so given the angle 35 degrees
we can work out r.
I get 3,654,255 metres.
2 X pi X r
A spreadsheet will work the whole thing out for you, but note that Microsoft Excel's sine function works in radians, not degrees. To convert the angle to radians, multiply by pi/180.
If my working is correct, you can use this Excel formula to calculate the length around the Earth of the 55 degree parallel, assuming that the Earth is a perfect sphere (which it almost is, but only almost):
=(SIN(35*PI()/180)*6371000*2*PI())
which gives me about 22,960,364 metres, very roughly half the circumference of one of the meridians.
Dividing that by 360 X 60 X 60 gives the distance covered by one second of in the UK - about 18 metres. So 0.001 seconds of longitude covers about 2 centimetres east to west and 0.0001 seconds covers about two millimetres. If I'm closer to Equator, the length covered will be bigger. If I'm nearer to the North pole, it will be smaller.
If my GNSS receiver is accurate to two or three centimetres and I'm working in the UK, I should believe the first two decimal places of the seconds value of the longitude and be a bit suspicious of the third decimal place.
If we only move over a short distance we can ignore the fact that Earth is round. We do this all the time. If you measure the width of the room you are sitting in with a tape measure you don't worry that the floor is curved, following the curve of the Earth.
If we know the longitude and latitude of two points on the Earth's surface, we can find the distance north to south between them and the distance east to west. If the two points are close enough we can ignore the curvature and figure out the distance between them, but how close is close enough?
My GPS devices are only accurate to about two centimetres, so once the difference gets significantly less than that, I can ignore the effect of the curvature.
We can use stuff we learned at school to calculate the distance between the two points.
We have a right-angled triangle. The distance between point 1 and point 2 is the length h of the longest side, the hyptenuse. We know the length of the two shorter sides. We can calculate h using Pythagoras' Theorem:
h2 = (distance ns)2 + (distance ew)2
so h is
square root of((distance ns)2 + (distance ew)2)
If the two points are at different heights, you can use the three-dimensional version of Pythagoras' Theorem - square the differences between all three measures and take the square root of the sum. So, that's a simple variant on the two-dimensional case.
Your Excel spreadsheet has a gadget SQRT() which will work out the square root for you.
That approach only works across a flat surface, so we have to know when we can ignore the Earth's curvature. We can use this diagram to figure that out:
As the two points get closer, the angle between them gets smaller. The distance around the curve becomes very close to the distance along the straight line that joins them, and we can ignore the difference.
The distance around the curve is:
(2 * pi * radius of Earth * angle in degrees) / 360
The sine of an angle in a right-angled triangle is:
(length of opposite side) / (length of hypotenuse)
so the length d is:
sine(a/2) X 6,371,000 metres
The length of the straight line joining the two points is twice that.
If you do the maths, you can find the discrepancy at various angles. According to my calculations:
| angle | 0.1° | 0.2° | 0.3° |
| distance around the curve | 11,119.493 | 22,238.985 | 33,358.478 |
| distance in a straight line | 1119.491 | 22,238.974 | 33,358.440 |
| difference | 0.001 | 0.011 | 0.038 |
So a difference in latitude of 0.2° covers about twenty kilometres along the ground and the curvature of the Earth over that distance produces a discrepancy no more than one centimetre, which is less than the resolution of my equipment. Above that distance, I have to worry about the curvature.
For longitude, the distance covered by an angle depends on the latitude, as we saw earlier, so the calculation is a little bit more complicated.
| <-- Previous | Contents Page | Next --> |
Copyright © Merrow Internet Services Ltd 2024